プロトレーダーも活用するFXのサイクル理論とは？

FXで利益をあげるには、チャートを分析して相場全体の流れを把握するのが基本となります。

サイクル理論はチャート分析の手法の一つとして、プロトレーダーをはじめ、多くのトレーダーに用いられています。

このサイクル理論への理解が深まれば、相場環境の分析はもちろん、エントリーポイントや損切り・利確の判断に役立てることができると思います。

サイクル理論とは

まずはサイクル理論の基本を理解しておきましょう。

FXの相場は常に上昇と下降を繰り返していて、この周期を「サイクル」と呼びます。

サイクル理論とは、サイクルに一定のパターンがあることに注目しそれを取引に活用する方法のことです。

このサイクル理論では「安値から次の安値までを1つのサイクル」と定義しているので、チャートの形が必ず高値を経由して山のような形になります。

サイクル理論を活用することで、チャートの流れが読みやすくなってFXでの利益を出しやすくなるのです。

サイクル理論の2つの形状・タイプ

サイクル理論は「ライトトランスレーション」と「レフトトランスレーション」の2つの形があって、それを分析していくことで売買のタイミングの判断に利用することができます。

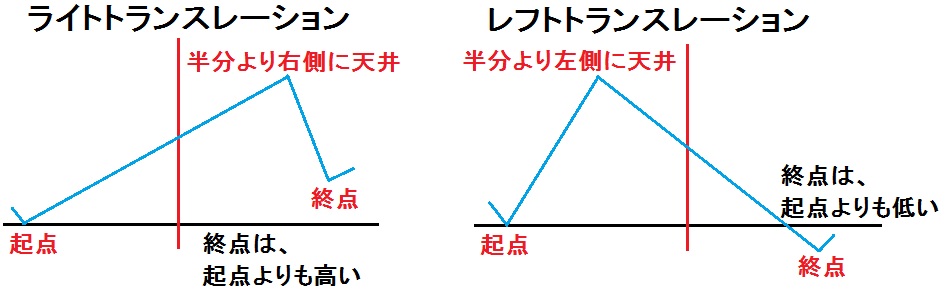
ライトトランスレーション

ライトトランスレーションとは、取引開始時の安値よりも切りあがる価格で次の安値が訪れるサイクルの形をいいます。

高値がサイクルの中間よりも時系列で後方（右側）に位置するのが特徴です。

チャート上では山が右寄りに形成されるのでライトトランスレーションと呼ばれています。

このライトトランスレーションが形成される時は、上昇トレンドになっていて買いの優位性が高い状態となります。

サイクルを見つけ、安値を更新していないことを確認した上で買い注文を入れるのが基本的なエントリーのスタイルになります。

損切りポイントは、起点を割り込んで安値を更新したタイミングとなります。

レフトトランスレーション

レフトトランスレーションとは、取引開始時の安値よりも切り下がる価格で次の安値が訪れるサイクルの形をいいます。

高値がサイクルの中間より前方（左側）に位置するのが特徴です。

チャート上では山が左寄りに形成されるのでレフトトランスレーションと呼ばれています。

このレフトトランスレーションが形成されるときは、下降トレンドになっていて売りの優位性が高い状態となります。

サイクルを見つけ、高値を更新していないことを確認した上で売り注文を入れるのが基本的なエントリーのスタイルになります。

損切りポイントは、起点を上回り高値を更新したタイミングとなります。

サイクル理論の7つの種類

1, 1dayサイクル

これは1日で完結しますので1時間足以下を使ったトレードスタイルで使用されます。

2, 4H(アルファ)サイクル

4Hサイクルは5～8日程度を1周期とするサイクルで、主に4時間足チャートでサイクルを確認します。

デイトレードのような短期的な取引をメインとするトレーダーに使われるサイクルです。

3, トレーディングサイクル

トレーディングサイクルは10～18日程度を1周期とするサイクルです。

4, メジャーサイクル

メジャーサイクルは、20～35日を1周期とするサイクルで、主に日足チャートでサイクルを確認します。

ハーフプライマリーサイクルと呼ばれることもあり、プライマリーサイクルと組み合わせて活用するケースが多くなっています。

5, プライマリーサイクル

プライマリーサイクルは、18～30週を1周期とするサイクルで、主に週足チャートでサイクルを確認します。

プライマリーサイクルは、スイングトレードを行うトレーダーにとって使用頻度の高いものとなっています。

6, 中間(季節)サイクル

中間サイクルは12～20か月程度を1周期とするサイクルです。

7, 長期サイクル

長期サイクルは40～100か月を1周期とするサイクルです。

サイクル理論周期の数え方

サイクル理論の周期はローソク足を使用して数えます。

使用する時間足や1周期あたりのローソク足の本数は変わります。

4Hサイクルであれば4時間足60〜80本前後、メジャーサイクルは日足35〜45本前後、プライマリーサイクルは週足15〜21本前後を1つとして波形をつくるのが一般的です。

80％ほどの確率でこのような周期があてはまるといわれています。

大きなサイクルから分析を行う

相場の流れを見ていく時と同じで、サイクル理論を使う時も大きなサイクルから分析を行います。

上位足のサイクルのほうが、優位性が高く信頼できるサイクルとだからです。

サイクル理論をトレードで使う場合には「1つの大きなサイクルの中に複数の小さなサイクルがある」ことを意識しましょう。

例えば、メジャーサイクルの中に4Hサイクルが2〜3個含まれるケースが多いです。

常に上昇と下降を繰り返すFX相場の中に規則性を見つけ、取引に活用することができるのがサイクル理論です。

うまく活用できれば、相場のトレンドを把握でき、適切なタイミングでの売買につなげられます。

但し、テクニカル分析においては一つの方法だけで実践するのはリスクが高いのも事実です。

あくまでも相場全体の流れを把握することに優れた理論だと位置づけ、精度の高いエントリーポイントを探るためには他のテクニカル指標との併用が必須だと思います。